INTRODUCTION
It has been observed that whenever a force acts on a body, and the body undergoes some displacement, some work is said to be done. Mathematically, if a force (P) acting on a body displaces it through a distance (s), then
Workdone = Force × Distance = P × s
But, sometimes, the body does not move in the direction of force (or in other words, the force does not act in the direction of motion of the body). In such a case,
Workdone = Component of the force in thedirection of motion × Distance= P cos è × s where è is the inclination between the line of action of the force and the direction of the motion of the body.
A little consideration will show that
1. If the value of è is between 0° and 90°, some work is done.
2. If the value of è is 90°, then no work is done (because cos 90° = 0).
3. If the value of è is between 90° and 180°, the body will move in the opposite direction and work is called as negative.
CONCEPT OF VIRTUAL WORK
In the previous article, we have discussed that the work done by a force is equal to the force multiplied by the distance through which the body has moved in the direction of the force. But if the body is in equilibrium, under the action of a system of forces, the work done is zero. If we assume that the body, in equilibrium, undergoes an infinite small imaginary displacement (known as virtual displacement) some work will be imagined to be done. Such an imaginary work is called virtual work. This concept, of virtual work, is very useful in finding out the unknown forces in structures.
Note. The term ‘virtual’ is used to stress its purely hypothetical nature, as we do not actually displace the system. We only imagine, as to what would happen, if the system is displaced.
PRINCIPLE OF VIRTUAL WORK
It states, “If a system of forces acting on a body or a system of bodies be in equilibrium, and the system be imagined to undergo a small displacement consistent with the geometrical conditions, then the algebraic sum of the virtual works done by all the forces of the system is zero.”
Proof. Consider a body at O, subjected to a force P inclined at angle è with X–X axis as shown in Fig. 16.1.
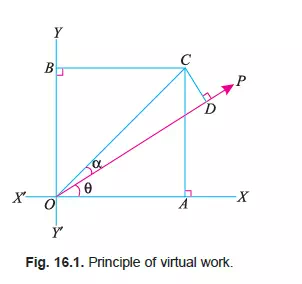
PX = Component of the force along X–X axis, and
PY = Component of the force along Y–Y axis.
From the geometry of the figure, we find that
PX = P cos è and
PY = P sin è
Now consider the body to move from O to some other point C, under the action of the force P, such that the line OC makes an angle á with the direction of the force. Now draw
CA and CB perpendiculars to OX and OY respectively as shown in Fig. 16.1.


SIGN CONVENTIONS
Though there are different sign conventions for finding out the virtual works done in different books, yet we shall use the following sign conventions, which are internationally recognised.
1. Upward forces are considered as positive, whereas the downwards as negative.
2. Forces acting towards right are considered as positive, whereas those towards left as negative.
3. Forces acting in the clockwise direction are considered as positive, whereas the anticlockswise as negative.
4. Tensile forces are considered as positive whereas the compressive as negative.
APPLICATIONS OF THE PRINCIPLE OF VIRTUAL WORK
The principle of virtual work has very wide applications. But the following are important from the subject point of view;
1. Beams
2. Lifting machine.
3. Framed structures.
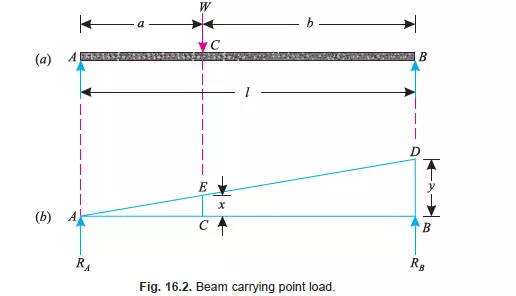
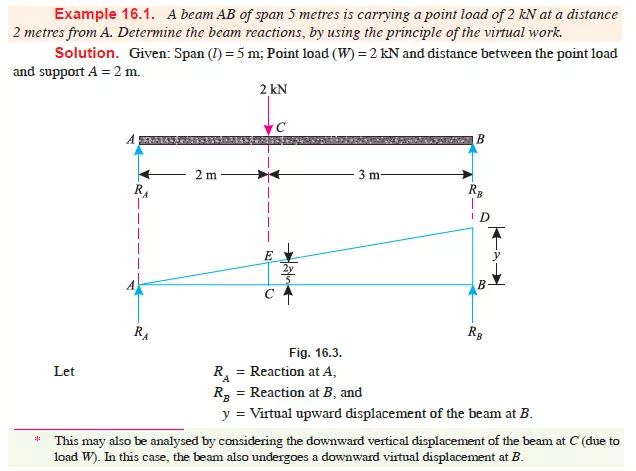
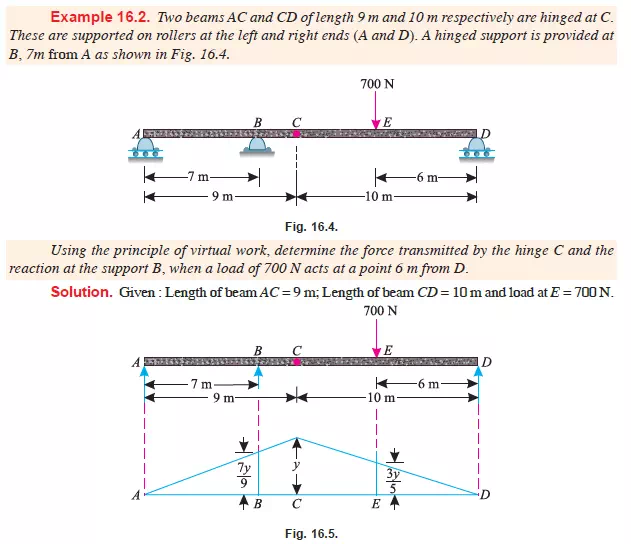
APPLICATION OF THE PRINCIPLE OF VIRTUAL WORK ON BEAMS
CARRYING POINT LOAD