Lack ofadequate data normally precludes development ofunit hydrographscovering a wide range ofdurations for a given catchment. Undersuch conditions aD hour unit hydrograph is used to develop unit hydrographs of differing durations nD. Two methods are available for this purpose.
Method of Superposition
If a D-h unit hydrograph is available and it is desired todevelop a unit hydrograph of nDh, where n isan integer, it is easily accomplished by superposing n unit hydrograph with each graph separated from the previous on by D-h.
Example 1
The ordinates of a 6-h unit hydrograph are given
| Time | (h) | 0 | 6 | 12 | 18 | 24 | 30 |
| Ordinate of 6-h UH | (m3/s) | 0 | 20 | 60 | 150 | 120 | 90 |
| Time | (h) | 36 | 42 | 48 | 54 | 60 | 66 |
| Ordinate of 6-h UH | (m3/s) | 66 | 50 | 32 | 20 | 10 | 0 |
Derive a 12-h unit hydrograph for the catchment.
Answer
| C1 | C2 | C3 | C4= C2+C3 | C5 = (C4/(12/6)) |
| Time | Ordinate of6-h UH | Ordinates of 6-h UHlagged by 6-h | C5 = (C4/2) | |
| Ordinates of 12-h UH | ||||
| h | m3/s | m3/s | m3/s | m3/s |
| 0 | 0 | 0 | 0 | |
| 6 | 20 | 0 | 20 | 10 |
| 12 | 60 | 20 | 80 | 40 |
| 18 | 150 | 60 | 210 | 105 |
| 24 | 120 | 150 | 270 | 135 |
| 30 | 90 | 120 | 210 | 105 |
| 36 | 66 | 90 | 156 | 78 |
| 42 | 50 | 66 | 116 | 58 |
| 48 | 32 | 50 | 82 | 41 |
| 54 | 20 | 32 | 52 | 26 |
| 60 | 10 | 20 | 30 | 15 |
| 66 | 0 | 10 | 10 | 5 |
| 72 | 0 | 0 | 0 |
S-curve
If it is desired to develop a unit hydrograph of durationmD, where m is a fraction, the method of superposition cannot be used. A different technique known as the S-curve method is adopted in such cases, and this method isapplicable forrational values of m.
The S-curve, also known as S-hydrograph is a hydrograph produced by a continuous effective rainfall at a constant rate for an infinite period. It is a curve obtained by summation of an infinite series of D-h unit hydrographs spaced D-hapart.
Fig .1 shows such a series of D-hhydrograph arranged with their starting points D-hapart.
At any given time the ordinates of the various curves occurring at that time coordinate are summed up to obtain ordinates of the S-curve. A smooth curve through these ordinate results in an S-shaped curve called S-curve.
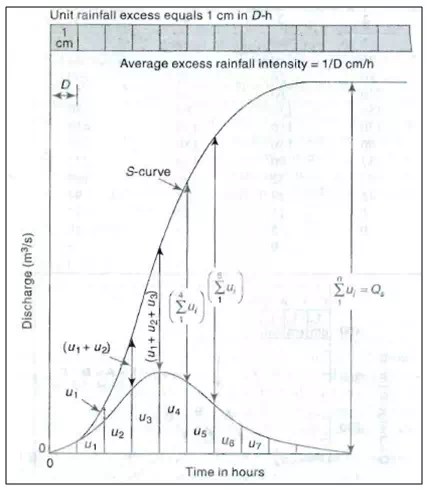
Fig. .1S-curve.
This S-curve is due to a D-h unit hydrograph. It has an initial steep portion and reaches a maximum equilibrium discharge at a time equal to the first unit hydrograph. The average intensity of ER producing the S-curve is 1/D cm/h and the equilibrium discharge,
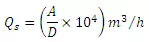
Where A is area of catchment in km2 and D is duration in hours of ER of the unit hydrograph used in deriving the S-curve.
By definition an S-curve is obtained by adding a string of D-h unit hydrographs each lagged by D-hours from one another. Further, if Tb = base period of the unit hydrograph, addition of only Tb/D unit hydrographs are sufficient to obtain the S-curve. However, an easier procedure based on the basic property of the S-curve is available for the construction of S-curves.
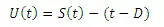
or
 (26.1)
(26.1)
The term S (t-D)could be called S-curve addition at time t
For all
Example 2
The ordinate of 2-h unit hydrograph of a basin are given:
| Time | (h) | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| 2-h UH Ordinates | (m3/s) | 0 | 25 | 100 | 160 | 190 | 170 | 110 |
| Time | (h) | 14 | 16 | 18 | 20 | 22 | 24 | 26 |
| 2-h UH Ordinates | (m3/s) | 70 | 30 | 20 | 6 | 0 | 0 | 0 |
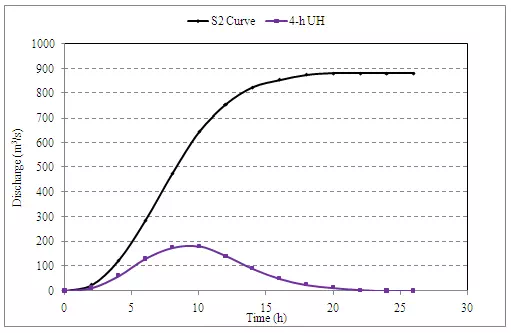
Compute a 4-h unit hydrograph ordinate and plot: (i) the S-curve (ii) the 4-h UG
| C1 | C2 | C3 | C4 | C5 | C6 = C4-C5 | C7 = C6/ (4/2) |
| Time | 2-h UH Ordinates | S curve addition | S2 curve ordinate | S2 curve lagged by 4 h | DRH of (4/2)= 2 cm | 4-h UH Ordinates |
| h | m3/s | m3/s | m3/s | |||
| 0 | 0 | 0 | 0 | 0 | 0.0 | |
| 2 | 25 | 0 | 25 | 25 | 12.5 | |
| 4 | 100 | 25 | 125 | 0 | 125 | 62.5 |
| 6 | 160 | 125 | 285 | 25 | 260 | 130.0 |
| 8 | 190 | 285 | 475 | 125 | 350 | 175.0 |
| 10 | 170 | 475 | 645 | 285 | 360 | 180.0 |
| 12 | 110 | 645 | 755 | 475 | 280 | 140.0 |
| 14 | 70 | 755 | 825 | 645 | 180 | 90.0 |
| 16 | 30 | 825 | 855 | 755 | 100 | 50.0 |
| 18 | 20 | 855 | 875 | 825 | 50 | 25.0 |
| 20 | 6 | 875 | 881 | 855 | 26 | 13.0 |
| 22 | 0 | 881 | 881 | 875 | 6 | 3.0 |
| 24 | 0 | 881 | 881 | 881 | 0 | 0.0 |
| 26 | 0 | 881 | 881 | 881 | 0 | 0.0 |