Shear strength

If a soil specimen is subjected to shear stress the shear stress-strain diagram may look like one of the curves in Figure 8.25, depending upon the soil conditions. A highly cemented soil will result in a well defined failure point as shown by curve A. Loose soil may not show any definite failure point and the stress may increase exponentially with strain reaching some maximum value as shown by curve B. Curve C is for a soil that is well compacted but not cemented.

The soil strength refers to the value of the shear stress on a plane within the soil sample where soil failure has taken place either by rupture or breakage. For curves A and C this point is clearly defined but for curve B soil failure is not distinct. In the case of curve C the failure is considered to have taken place by yielding or plastic flow and the asymptotic value of shear stress is taken as the shear strength for this case. The shear stress-strain curves shown in Figure 8.25 are for a given normal stress on the sample. If the normal stress is changed the shear stress-strain diagram will change and consequently the value of the maximum shear stress will also change. An increase in the normal stress would cause an increase in maximum shear. Therefore, the shear strength is a function of the normal stress on the failure plane.

Mohr-Coulomb failure theory states that failure in a material occurs if the shear stress on any plane equals the shear strength of the material. Furthermore, the shear strength (s) along any plane is a function of the normal stress (σ) on the plane, as shown below:

Coulomb, in 1776, conducted experiments to determine the maximum shear stress that could be applied on a plane within a sample of soil at varying levels of normal stress. He plotted the maximum shear stress values at failure against the corresponding normal stress on the failure plane and suggested the following linear relationship:

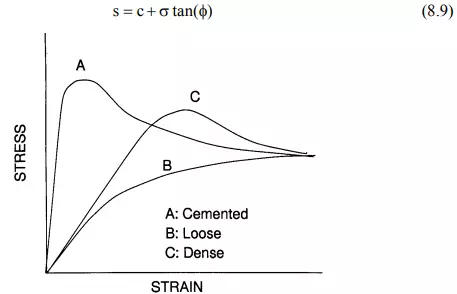
Figure 8.25 – Typical shear stress-strain diagrams for soils in three conditions.

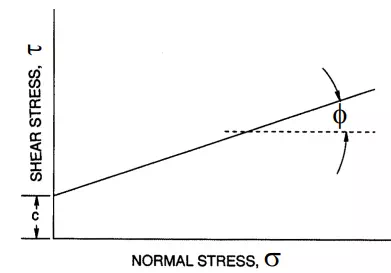
Figure 8.26 – Soil failure envelopes.

The Coulomb criterion is shown as a straight line in Figure 8.26, with an intercept on the shear stress (τ) axis equal to c and a slope equal to tan φ. The quantities c and φ are material properties frequently called cohesion and angle of internal friction, respectively. The shear strength as defined by Equation 8.9 represents the maximum shear stress that may be sustained on any plane in a given material. The strength function is called the failure envelope since it defines the limiting stress.